|
|
Gels are crosslinked-polymeric networks immersed in a solvent, whose size can change using
external stimuli. Microgels are gels in the colloidal domain.
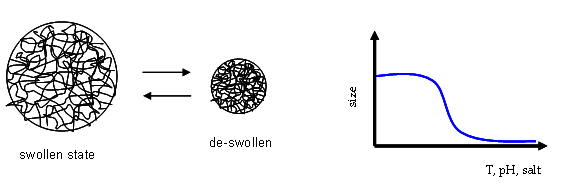
Fig.1. Sketch of the behavior of a microgel particle. Its size can be controlled
using external variables such as Temperature, pH or salt concentration.
From a fundamental point of view, they have been treated as colloidal hard
spheres and when concentrated, they exhibit a liquid, crystal and glassy phases depending
solely on the volume fraction of the particles, Φ=np V1p,
with np the number density of particles
and V1p the volume of a single particle, as is sketched in Fig.2A. However, there are
several experimental evidences which suggest that, in certain conditions, microgel suspensions
can display a considerably richer and more fascinating behavior, as is shown in Fig.2B for a
typical thermosensitive polymer NIPAM microgel copolymerized with a pH-sensitive group, acrylic
acid. As the acrylic groups get ionized by increasing the pH, the crystalline region narrows down
and, eventually, disappears.
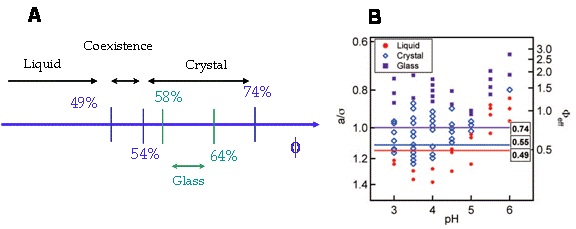
Fig.2. A) Classical phase diagram for hard spheres. In the absence of interaction,
the volume fraction is the only parameter relevant in the phase transition. B) Experimental
phase behavior of a NIPAM-Acc system. As the Acc ionizes, the crystalline region
shrinks and disappears for high enough pH.
Taken from Meng et al, J.Phys. Chem, B, 113, 4590, 2009.
Colloidal phase behavior and phase transitions.
The aim of this project is to study the phase behavior,
including the glassy phase, of a system of microgel particles.
By changing the particle size we would be able to change the volume fraction
of the system and thus, transitions can be induced within the same experimental
sample in a very elegant manner.
Our experimental system is a NIPAM microgel copolymerized with acrylic acid (2%). Thus,
the system is both sensitive to temperature and pH changes in the sample.
The phase behavior of the system as a function of the generalized
volume fraction &xi=npV c ~ 0
with V c ~ 0 the volume of one particle in the dilute state, is shown
in Fig. 3. At low &xi, the system shows an isotropic, liquid phase. When &xi is increased,
the system forms a crystalline phase characterized by Bragg reflections. At higher
concentrations, the Bragg reflections disappear and we observe a glassy phase
(the color shift from green to blue is a signature of the decrease in the nearest
neighbor distance, as expected since the particle concentration increases).

Fig.3. Phase behavior of the NIPAM-Acc. The system shows
liquid,
crystalline and glassy phases similar to hard spheres.
Hydrostatic pressure as a tuning variable for particle size.
We use a novel approach based on tuning the particle size using hydrostatic pressure, P.
As P increases, the interaction between the polymer and the solvent becomes increasingly
unfavorable and the particle deswells, as is shown in Fig.4.
Its role is similar to that of Temperature with the advantage that hydrostatic pressure
changes transmit homogeneously throughout the sample and are achieved faster.

Fig.4. Dependence of the particle size with hydrostatic pressure. The pressure
changes the miscibility of the polymer on the solvent and, as it increases, the
particle deswells.
Neutron Scattering as a tool for elucidating structural and dynamical
properties of the system.
The characteristic size of the microgel particles (~100 nm) makes
Small
Angle Neutron Scattering (SANS) a suitable technique to study and
characterize the different phases observed in the system. In any scattering
experiment, the collected intensity has an angular dependence
which can be expressed as:
I(q) ~ P(q) S(q)
where q is the scattering vector defined as the difference between
the incident and the scattered wave vector and thus depends
on the scattering angle, P(q) is called the form factor and accounts
for particle properties (geometry, size…) and S(q) is called the structure
factor and accounts for the structural properties of the system.
We first measure the form factor in dilute conditions, where S(q) = 1, and that
allow us to obtain an independent measurement of the form factor of the particles. This is
shown in Fig.5

Fig.5. Particle form factor as a function of hydrostatic pressure.
The solid lines represent the expected form factors for hard spheres at
a = 145nm (corresponding to particle size at P =0)
and a = 90 nm (corresponding to particle size at P=350nm)
The form factor displaces to smaller q’s as the particle size increases
(hydrostatic pressure decreasing) as expected from Fig.4. The form
factor can be described using a polydisperse core-shell model in which the core is
represented as a hard sphere of radius R and for the shell,
a Gaussian function of characteristic size &sigmasurf is used. In addition, the internal
structure of the particles is taken into account using a Lorentzian term of
characteristic length &sigmaf [see Stiger et al]:
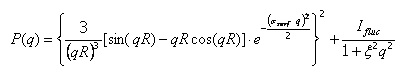
Thus, by measuring I(q) (Fig.6a) we can calculate the structure
factor of the system dividing by P(q). This is presented in Fig.6(b).
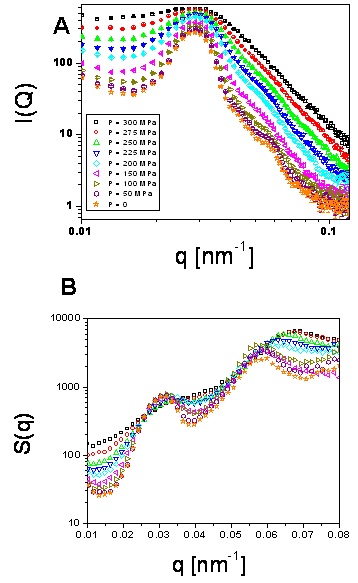
Fig.6. (a) Scattered intensity and (b) structure factor vs q at different
hydrostatic pressures for volume fraction » 0.68
These structure factors are considerably different from those of a monodisperse
system of hard spheres at similar volume fractions. A possible reason for this difference
[Stieger et al] is the inadequacy of the form factor used to obtain the structure
factor from the scattered intensity, since at high volume fractions
the particles would deform and interpenetrate. However, this procedure seems
to yield reasonable results when comparing experiment and theoretical expectation
for crystal samples, in which the volume fraction is slightly smaller (see Fig.3).
An alternative possibility is an increased polydispersity of
the sample with volume fraction, for sufficiently high volume fractions.
In the case of polydisperse hard-sphere systems, the structure factor exhibits
a nearest neighbor peak which is smaller than the plateau at higher q [Scheffold],
similar of what we observe experimentally.
Some useful references:
- J.J. Lietor-Santos, B. Sierra-Martin, R. Vavrin, Z. Hu, U. Gasser, A. Fernandez-Nieves,
Crystal structure of highly concentrated,
ionic microgel suspensions studied by neutron scattering, Physical Review E 79, 051403 (2009).
- Z.Meng, J.K.Cho, V.Breedveld, L.A.Lyon, Physical Aging and Phase Behavior
of Multirresponsive Microgel Colloidal
Dispersion, The Journal Physical of Chemistry B, 113, 4590 (2009).
- W.Stieger, W.Richtering, J.S.Pedersen et al, Small angle neutron scattering study
of structural changes in temperature sensitive microgel colloids, Journal
of Chemical Physics, 120, 6197 (2004).
- F.Scheffold, T.G.Mason,Scattering from highly packed disorder
colloids, Journal of Physics- Condensed Matter, 21, 332102 (2009).
Contact Information:
Juan Jose Lietor-Santos
Office: Boggs Building, Room B-54
Email address: jjlietors [at] gatech.edu
Phone: 404-385-3681
|
|



















