Shear and compression of soft materials – How different can they be?

Juan Jose Lietor-Santos , Benjamin Sierra-Martin, Alberto Fernandez-Nieves

School of Physics, Georgia Institute of Technology, Atlanta, Georgia, 30332.

Famous physicist Richard Feynman said: “If, in some cataclysm, all of scientific knowledge were to be destroyed and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis (or the atomic fact, or whatever you wish to call it) that all things are made of atoms -  little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied” [1].

In other words, matter is made of atoms and they repel if too close and attract if far away. This behavior is reminiscent of the behavior of springs, which stretch upon compression and compress upon stretching. We can then imagine the atoms in a material like tiny spherical balls that are connected by springs. This idea of modeling the atoms and their interactions as balls and springs was first formulated by Albert Einstein when trying to explain the thermodynamic behavior of solids [2]. In spite of its very simplistic approach, the ball and spring model is able to qualitatively explain many behaviors of solid materials. Take for instance the example of a block resting on a table, as schematically shown in Fig.1. We all know that the Earth exerts an attractive force over the block that we call the “gravitational force” or weight, which in fact we can calculate as F_g = mg, with g = 9.81 m/s² and m the mass of the block. From the fact that the block is at rest on the table, we know there must be another force compensating the gravitational force; otherwise the box will fall down. Since the only other object interacting with the block is the table, we conclude that this compensating force must be exerted by the table on the block. This force is often referred to as the normal force. How can we think about the origin of this force? We can recur to a ball and spring model for the table: Picture the table as a set of balls (atoms) and springs (interactions between the atoms). The normal force simply results from the compression of the balls of the table under the weight of the block. It is the restoring force that results from squeezing the atoms in the table together.

Fig.1 A box lies on a table. The inset represents an schematic view of the interatomic interaction between the box and the table.

Let us go one step further. Let’s imagine that we are trying to move this block along the table. We will see that for the block to move at a constant speed, we need to always keep applying a horizontal force in the direction of motion. In other words, if we do not apply this force, the block will stop moving. Why? The only explanation is that there must be another horizontal force arising from the interaction between the block and the table, which acts in the direction opposite to the direction of motion. We can again understand this force by recalling the ball and spring model of a solid: The springs connecting the balls of the block to the balls of the table are stretched as one moves relative to the other resulting in a restoring force that we call friction force, f. For many objects and many surfaces, this force is proportional to the normal force, F_N, with a proportionality coefficient, µ, the friction coefficient, which is constant for a given pair of surfaces in contact. Then:

f = µ F_N

Typical values for µ are in the range [0.1, 1], indicating that f is at most an order of magnitude smaller than F_N, which further reflects that shearing a solid (i.e. dragging balls of the block parallel to the balls of the table) is typically easier to achieve than compressing it (i.e. bringing the balls of the table closer together).

This feature is also exhibited by disordered soft materials, like emulsions and foams, which are made of drops and bubbles, respectively. Since these are deformable, at high concentrations they are no longer spherical but rather faceted, as shown in Figure 2. As it turns out, the elasticity of emulsions and foams arises from the storage of energy at the interfaces between drops and bubbles; the larger the packing fraction, the larger the faceting and thus the larger the interfacial energy. Interestingly, the volume of the individual constituents does not change and it is only the shape change that contributes to their elasticity. We can account for this by modeling the contact region between neighbor drops and bubbles as if mediated by a spring. Therefore, a compressed emulsion or foam can be viewed as a random arrangement of springs, with a ratio between the shear modulus, accounting for the material response to shear deformations, and the bulk modulus, accounting for the material response to a compression, in the range [0.1,0.7] [3,4].

Fig.2. a) Packed emulsion, b) Packed foam.

The situation is quite different if the individual constituents are compressible. This is the case for soft particles like microgels, which are cross-linked polymer networks that are able to transition reversibly from a collapsed to a swollen state in response to changes in temperature, pH or hydrostatic pressure, as shown in Fig. 3 [5]. Since microgels swell or deswell by absorbing or releasing solvent, they are compressible by construction, and as their number per unit volume increases, the individual particles can be compressed by the presence of their neighbors.

Fig.3. Schematic representation of the swelling transition of microgel particles.

For low volume fractions, microgel suspensions and emulsions behave similarly in terms of their elasticity, where the Laplace pressure of the emulsions is substituted by some contact modulus extracted from the Young modulus of the individual particle. This analogy, however, is broken down as the volume fraction is increased and the particles are forced to touch one another. In this regime, we show that the relevant elastic scale of the system is set by the microgel bulk modulus, K_p, that we determine using dextran solutions of known osmotic pressure [6]. K_p determine the volume fraction dependence of the bulk and the shear modulus of the suspension.

Since the suspension can be packed beyond the hard sphere limit, due to the softness of the particles, we characterize the concentration of the suspension using a generalized volume fraction, z = nV, with n the particle number density and V the volume of a particle measured in dilute conditions. Values of z > 1, imply that the microgels “fill space” and must have shrunken in order to fit in the available space. It is important to note that z is equal to the suspension volume fractions at low concentration.

We measure the osmotic pressure, P, of suspensions with different amounts of cross-link molecules using membrane osmometry. We find that P increases with z and with the particle stiffness, as characterized by the amount of cross-link. From the osmotic pressure measurements, we can obtain the bulk modulus of the suspension, or the inverse compressibility as:

When we normalized the bulk modulus of suspensions with different amounts of crosslink by the particle bulk modulus, we obtain that K scales onto a single curve and remains constant for volume fractions where particle deformation is expected, as shown in Fig.4. This emphasizes that K_p sets the relevant elastic scale and the volume fraction dependence. Furthermore, we note that P/K_p » 1 for z » 1, which indicates that the osmotic pressure exerted by the suspension on each particle is of the same order of magnitude of the particle stiffness around the packing fraction in which the microgels are physically in contact. In other words, these results seem to show that particle deswelling cannot take place before the microgels are physically touching each other.

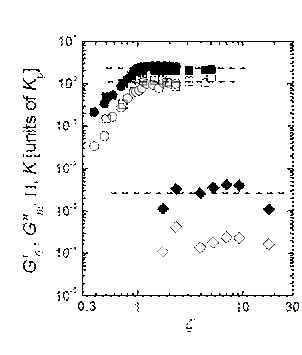
Fig.4. Bulk modulus (n,l), osmotic pressure (o,ˇ), plateau shear modulus (t), and G’’_m

(Ż), normalized by the bulk modulus of individual microgels vs ζ . Squares and circles represent microgel systems with different stiffness.

We also perform rheological characterization of the system to determine its shear response. Specifically, we determine the viscous, G’’, and the elastic moduli, G’, of the suspension as a function of frequency for several values of z. We characterize the resistance to shear of the suspension using the plateau modulus, G’_o = G’ (w = 1 rad/s) and the value of the viscous loss at its minimum, G’’­_m. Remarkably, both moduli remain constant when normalized by the bulk modulus of the particles as shown in Fig.4. This truly emphasizes the crucial role played by the particle bulk modulus which not only controls the bulk modulus of the suspension but also its shear response [7]. In a way, these results are analogous to the way in which the normal force ultimately determines the solid-solid friction force through the friction coefficient.

This result is even more striking if we follow this analogy and notice that K is almost three orders of magnitude larger than G’₀, and that this ratio remains up to the highest z we probed. This is in stark contrast to what is observed for systems based on incompressible particles like emulsions and foams, somehow suggesting that there is something intrinsically different when the system is made of compressible objects. This astonishing result might have implications for designing new materials with an unusual different response to shear and compression.

References:

1.- R.P.Feynman, R.B.Leighton and M.Sands, The Feynman Lectures in Physics, 1965, Addison-Wesley, Palo Alto, CA, USA.

2.- A.Einstein, Ann. Der Physik, 22, 180, 1907.

3.- T.G.Mason, J.Bibette and D.A.Weitz, Phys. Rev. Lett., 75, 2051, 1995.

4.- R. Hohler, Y. Y. C. Sang, E. Lorenceau, and S. Cohen-Addad, Langmuir, 24, 418, 2008; S. Marze, M. Guillermic, and A. Saint-Jalmes, Soft Matter, 5, 1937, 2009.

5.- Microgel Suspensions: Fundamentals and Applications, edited by A. Fernandez-Nieves, H. M. Wyss, J. Mattsson, and D. A. Weitz, 2011, Wiley-VCH, Berlin, Germany.

6.-  B.Sierra-Martin, J.A. Frederick, Y.Laporte, G.Markoy, J.J. Lietor-Santos, A.Fernandez-Nieves, Coll. Polym. Sci., 289, 721, 2011.

7.- J.J.Lietor-Santos, B.Sierra-Martin, A.Fernandez-Nieves, Phys. Rev. E, 84, 060402(R), 2011.