|
|
Introduction
Microgel particle systems have attracted increasing interest in the field of Soft Condensed
Matter as their ability to swell or expand upon change of variables such as temperature, pH or ionic strength
allows studying a broad phase behavior in within a single sample [1-4]. Furthermore, due to their intra-particle
structure and uneven or discontinuous mass distribution, microgel particles can deform, interpenetrate or enhance their
polydispersity which ultimately results in a strikingly different phase behavior than typical hard sphere systems [5-7]. In this project
we study a recent class of thermally responsive microgel system where PEG is employed as cross-linker of linear PNiPAM. PEG is
a hydrophilic non-degradable polymer extensively used in bio-related materials as it is biocompatible, non-toxic, non-immunogenic
and soluble in water. Moreover, research on colloidal particles which are surface modified with PEG has drawn attention as
PEG facilitates control of protein adsorption and minimizes non-specific cell adhesion [8,9]. Thus PNiPAM-PEG microgels lay
a promising system that can be employed not only in fundamental research but also in bio- and nano-technological applications such
as drug delivery in biological systems [10].
Cross-linked PNiPAM-particles are soluble in water at temperatures below the Lower Critical Solution Temperature (LCST)
of PNiPAM at T ~ 33°C. In the fully swollen state at low temperatures their behavior varies from more polymer-like to more
colloid-like behavior depending on the cross-linking density [11]. As the temperature increases, the size of the PNiPAM-microgels
decreases continuously up to the LCST. Beyond the LCST the microgels collapse forming now more colloidal-type systems, which aggregate
unless they are stabilized in some way [12]. To PNiPAM-PEG particles, the hydrophilic properties of PEG at low temperatures differentiate
this system from other microgels. When the temperature is low enough, PEG chains protrude from the microgel network which results in
an uneven mass distribution dissimilar to typical microgel systems [13,14]. We employ Static and Dynamic Light Scattering (SLS and DLS)
to investigate the structure and dynamics of aqueous suspensions of these microgels at different volume fractions and at
different temperatures. Furthermore, we also employ Rheology to explore the mechanical properties of this particular class of microgel system.
SLS and DLS of PNiPAM-PEG microgel suspensions in the low-concentration regime.
We have characterized our PNiPAM-PEG microgel particles using SLS and DLS for temperatures, T, within the
range 20C ≤ T ≤ 46C. In all SLS experiments and at large enough q-vectors, the scattered intensity depends linearly
with q ² when displayed in a logarithmic-linear scale; this indicates that in the available q-range of our experiments
we access the Guinier region of the microgel form factor, as shown in Figure 1(a) [15]. Furthermore, the slope of the
scattered intensity increases when the temperature is increased, indicating the decrease in the particle size. Since our
suspensions are dilute, there are no spatial correlations between the particles and beside prefactors, the scattered intensity
I(q) corresponds to the microgel form factor, P(q). In the Guinier region, P(q) ~ exp(-Rg² q²/3) and therefore it is straightforward
to obtain the radius of gyration, Rg, for every temperature, which is shown in Figure 1(c) with open circles. We also quantify
the de-swelling behavior using DLS. We measure the intensity correlation functions, g2(τ) - 1, and find they exhibit
a linear dependence with the lag time, τ, when displayed in a logarithmic-linear scale. This indicates the exponential
character of these functions, as shown in Figure 1(b). Since the scattered intensity fluctuations are Gaussian, the
Siegert relation must be fulfilled: g2(τ) - 1 = g1(τ)², where g1(τ) is the field correlation
function. Then, g2(τ) - 1 ~ exp(-2τ/&tau0), where τ0 = 1/(q²D), with
D the diffusion coefficient [16]. The exponential
character of g1(τ) is suggestive of diffusion, which we further confirm by verifying that τ0 depends
linearly on q². The diffusion coefficient at each temperature is further related to the hydrodynamic
radius of the particles, Rh, invoking Stokes-Einstein: D = kBT/6πηRh, with kB the Boltzmann constant, T
the temperature and η the solvent viscosity. Consistent with the findings for the radius of gyration, we find
that Rh decreases with temperature down to a minimal size at the LCST, as shown in Figure 1(c) with closed circles.
Despite the behavior of Rh and Rg with temperature is remarkably similar, they have very different
magnitudes; the hydrodynamic radius is larger than the radius of gyration at all temperatures. This difference can
be attributed to an uneven distribution of cross-linker, which decreases from the center of the particle towards its
periphery [17]. Because of the higher density of PNIPAM within the core, the core scatters significantly more than
the low-density shell, and thus in SLS the radius of the cross-linked core is portrayed in contrast to DLS which
portrays the effective hydrodynamic radius. Note that above the LCST, the interaction between the particles
contains an attractive contribution. However, we do not observe aggregation, indicating there must also be
a repulsive contribution to the particle-particle interactions, which in our case results from the presence
of charge at the surface of the particles from the ionic initiator used in the microgel synthesis [11,17]. This
charge remains unscreened and provides suspension stability for T > LCST.
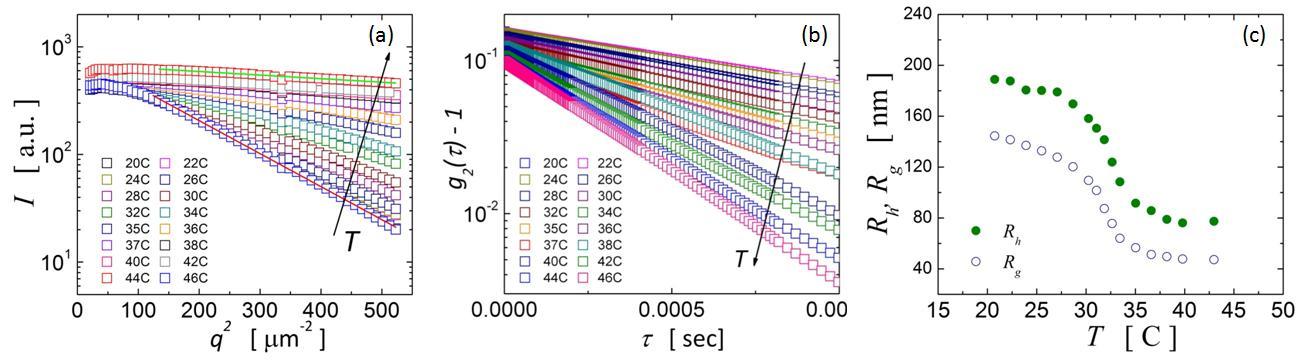
Figure 1. SLS intensity variation with the wave vector q (a) and DLS intensity
correlation functions (b) for PNiPAM-PEG microgel particles at different temperatures. Both, the DLS
hydrodynamic radius and the SLS radius of gyration gradually decrease with increasing
temperature up to a constant size above the LCST (c).
Statics, dynamics and mechanical properties of PNiPAM-PEG microgel suspensions in the high-concentration regime.
At high enough concentration of PNiPAM-PEG particles, the system eventually jams and a solid-like
structure is formed as shown in figure 2. We quantify the particle concentration by using a generalized volume fraction ξ=c(R(T)/R(T=46C))³ where
c is the microgel weight concentration, R(T) is the particle hydrodynamic radius at temperature T and R(T=46C) is the one
corresponding to T=46C. Note that the magnitude of ξ can be above unity, which suggests that at such volume fractions the
particles either shrink, interpenetrate or vary their shape, or all of them. Indeed, for &xi < 1 the system is at a liquid
state while at ξ > 1 the system is at a solid phase. Here our focus is to explore the structural, dynamic
and static properties of our samples in the solid state as this state is approached. Therefore
we study the phase behavior of PNiPAM-PEG microgel systems at extreme high concentrations.
As an example we draw our attention on suspensions at a volume fraction at &xi =1.5 and introduce the
behavior corresponding to the temperature range 20C ≤ T ≤ 32C. At these temperatures the
effective structure factor, Seff(q), displays a peak at a position where qpeak•Rh ~ π as
illustrated in figure 3. Despite
this hallmark indicates that the spatial configuration of our microgels is governed by their hydrodynamic radii, Seff(q) is
also characterized by a gradual decrease of the ratio Seff (q = qpeak)/Seff (q ~ 0) by decreasing
the temperature. This feature indicates a gradual loss of in the probability of two particles found at
distance ~ π/ qpeak which suggests a gradual structuring(unstructuring) of the system by
raising(decreasing) the temperature. Note that the effective structure factor is determined by the ratio
Seff(q)=(cconc/cdiluted)x(I(q)conc/I(q)diluted) where
cconc and cdiluted respectively are the mass
concentrations of the system at ξ=1.5 and the one corresponding to the diluted sample.
The magnitudes I(q)conc and I(q)diluted also respectively are the single static scattered
intensity of the system at ξ=1.5 and the one corresponding to the diluted sample. This protocol enables to
display the effective structure factor, Seff(q), where prefactors due, for example, to the microgel index of refraction
in the diluted, concentrated or different temperature states are omitted. Moreover, we consider that the single particle form
factor does not vary at the considered volume fraction ξ=1.5. Note that we take full advantage of the scattering set-up and
standard protocols are applied to obtain the single static intensity, I(q)conc, in fairly turbid systems [18].

Figure 2. PNiPAM-PEG microgel particles at a 40wt% concentration. At room temperature the particles
are swollen and the system exhibits the properties of a solid (a). When the temperature is raised up to T=40C, the
particle size is low enough so that a liquid state is reached (b). Note the different contrast of the suspension in
between (a) and (b) not only due to the different particle sizes but also due to different indexes of refraction as
the amount of solvent in the particles at swollen and de-swollen states is different.
At these conditions of temperature and volume fraction, DLS measurements are performed simultaneously
than SLS experiments yielding the intensity correlation function g2(τ) – 1 shown in figure 3. These correlation
functions exhibit a single decay regardless of the q-vector position and are stretched exponentials in character,
i.e. g2(τ) – 1 ~ βexp(-2(τ/&tau0)p) where β is the experimental intercept, p is the stretched exponent
and τ0 is the relaxation time. The normalized relaxation time τ0/τD, where &tauD
is the relaxation time
that corresponds to diffusive dynamics, varies with the q-vector in a similar fashion than the
effective structure factor Seff(q). Moreover, at all temperatures the stretched exponent p ~ 0.7. These features
are reminiscent of hard sphere systems [19], however, the ratio τ0/τD gradually decreases by decreasing temperature
as shown in figure 3 and therefore dynamics becomes faster and closer to diffusion for low temperature systems.
To gain further knowledge on PNiPAM-PEG microgel phase behavior, we perfom rheological experiments on
suspensions at different temperatures at ξ = 1.5 and focus on the frequency response of these systems. As shown
in figure 4, at high temperature elasticity clearly dominates over the viscous modulus and exhibits an onset to a frequency
independent plateau, hallmark to viscoelastic solids. However, the magnitude of the elastic modulus gradually decreases
by gradually decreasing the temperature down to a profile where the viscous modulus gains
authority over the elastic one. Additionally, the crossover time in between elastic
and viscous moduli gradually shifts to shorter frequencies and denotes that the system
relaxes faster at low temperatures which is as well pointed out by the different
ratios τ0/τD at high and low temperatures.
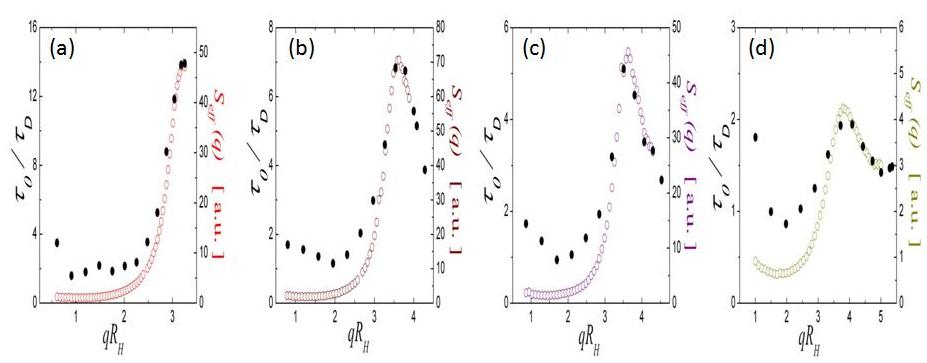
Figure 3. Effective structure factors, Seff(q) (right y-axis) and normalized relaxation
times τ0/τD (left y-axis)
of PNiPAM-PEG microgel suspensions at ξ = 1.5 and temperature T = 32C (a), T =28c (b), T = 22C(c), T = 17.5C (d).

Figure 4. Frequency response of PNiPAM-PEG microgels at ξ = 1.5 and at T = 32C (a), T = 28C (b), T =22C (c) and T =17.5C (d).
Elastic and viscous moduli are respectively represented by green and blue circles.
Outlook
We study highly concentrated suspensions of PNiPAM-PEG microgel systems through different invasive (Rheology) and non-invasive
(SLS and DLS) techniques at different temperatures. Despite at each temperature the response of the system exhibits common features, there
are remarkable differences that suggest a more structured system at high than low temperatures. Moreover, DLS and frequency response
experiments suggest that particle dynamics is faster at low than high temperature where the system displays longer relaxations. Such
behavior is striking as we focus on volume fractions ξ > 1, where an arrested glass-like state should be expected. To better
understand the nature of our suspensions we are currently expanding our studies to a larger spectrum of temperatures and volume
fractions. Howverer, the behavior of the system just at ξ = 1.5, suggests that the configuration of the particle plays a key role
as microgels reconfigure their intra-structure at each temperature, evidenced by DLS and SLS measurements
in dilute PNiPAM-PEG suspensions.
References
[1] G. Romeo, A. Fernandez-Nieves, H. W. Hyss, D. Acierno, D. A. Weitz, Temperature-Controlled Transitions Between Glass, Liquid, and Gel States in Dense p-NIPA Suspensions. Advanced Materials (accepted, published online April 2010).
[2] J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D.A. Weitz, Soft Colloids Make Strong Glasses. Nature, 2009, 462, 83-86.
[3] A. Fernandez-Nieves, A. Fernandez-Barbero, B. Vincent and F. J. de las Nieves, Reversible Aggregation of Soft Particles. Langmuir, 2001, 17 (6), 1841-1846.
[4] A. F. Routh and B. Vincent, Salt Induced Homoaggregation of Poly(N-isopropyacrylamide) Microgels. Langmuir, 2002, 18 (14), 5366-5369.
[5] B. H. Tan, K. C. Tam, Y. C. Lam and C. B. Tan, Osmotic Compressibility of Soft Colloidal Systems. Langmuir, 2005, 21, 4283-4290.
[6] M. Stieger, J. S. Pedersen, P. Linder, W. Richtering, Are thermoresponsive Microgels Model Systems for Concentrated suspensions? A Rheology and small-Angle Neutron scattering Study. Langmuir 2004, 20, 7283-7292.
[7] J.J. Lietor-Santos, C. Kim, M.L. Lynch, A. Fernandez-Nieves and D.A.Weitz, The Role of Polymer Polydispersity in Phase Separation and Gelation in Colloid-Polymer mixtures. Langmuir 2010, 26(5), 3174-3178.
[8] A. Revzin, R.J. Russel, V.K. Yadavalli, W.G. Koh, C. Deister, D.D: Hile, M.B. Mellott, M. Pishko, Fabrication of Poly(ethylene Glycol) Hydrogel Microstructures Using Photolithography. Langmuir 2001, 17, 5440-5447.
[9] E. Tziampazis, J. Kohn, P.V. Moghe, PEG-variant biomaterials as selectively adhesive protein templates: Model surfaces for controlled cell adhesion and migration. Biomaterials, 2000, 21, 511-520.
[10] J.H. Ward, N.A.J. Peppas, Preparation of Controlled Release Systems by Free-Radical UV polymerization in the presence of a drug. Journal of Controlled Release, 2001, 71 183-192
[11] H. Senff and W. Richtering, Influence of Cross-Link Density on Rheological Properties of Temperature-Sensitive Microgel Suspensions. Colloid and Polymer Science, 2000, 278(9), 830-840.
[12] E. Daly and B. Saunders, A Study of the Effect of Electrolyte on the Swelling and stability of Poly(N-isopropylacrylamide) Microgel dispersions. Langmuir, 2000, 5546-5552.
[13] T.G. Mason and M.Y. Lin, Density Profiles of Temperature-Sensitive Microgel Particles. Physical Review E, 2005, 71, 040801 1-4
[14] D. Gan and L.A. Lyon, Synthesis and Protein Adsoprtion Resistance of PEG-Modified Poly(N-isopropylacrylamide) Core/Shell Microgels. Macromolecules, 2002, 35, 9634-9639.
[15] A. Guinier and G. Fournet, Small-Angle Scattering of X-Rays. 1955, New York: Wiley Interscience.
[16] B.J. Berne and R. Pecora, Dynamic Light Scattering. 1976, New York: Wiley
[17] H. Senff and W. Richtering, Temperature sensitive microgel suspensions: Colloidal phase behavior and rheology of soft spheres. Journal of Chemical Physics, 1999. 111(4): p. 1705-1711.
[18] C. Urban and P. Schurtenberger, Characterization of Turbid Colloidal Suspensions Using Light Scattering Techniques Combined with Cross-Correlation Methods. Journal of colloid and Interface Science, 1998, 207, p. 150-158.
[19] P.N. Segre and P.N. Pusey, Scaling of the Dynamic Scattering Function of Concentrated Colloidal Suspensions. Physical Review Letters, 1996, 77(4), 771-774.
Contact Information:
Joaquim Clara-Rahola
Office: Boggs Building, Room B-55A
Email address: joaquim.clara-rahola [at] mail.gatech.edu
Phone: 404-385-3682
|
|



















