Structure of Complex Microgels and Microgel Suspensions

John S. Hyatt, Emily S. Herman, L. Andrew Lyon, Alberto Fernández-Nieves

Microgels are a class of particles defined by several characteristics. They are (like gels) crosslinked polymer networks. Also like gels, the polymers they are made of are mixed with and solvated by a liquid (as opposed to, say styrofoam or plastic bags). Unlike gels, however, they cannot be arbitrarily large; microgels are colloidal particles (i.e. small enough that they do not settle out of suspension in the solvating liquid). They are researched in a variety of contexts: in medicine, either as vectors for drug delivery or as matrices for cell growth and healing, in oil recovery, and in industry; they are also interesting from a fundamental physics point of view. Specifically, as soft particles, their phase behavior with varying concentration is strongly dependent on their softness and can be very different from the (very-well characterized) phase behavior of hard particles. I study microgels, and here is a short summary of some of my work, including one microgel system (pNIPAM-PEG-AAc) and one research tool (light- and neutron-scattering).

One particular system, a poly(N-isopropylacrylamide)-poly(ethyleneglycol)-acrylic acid (pNIPAM-PEG-AAc) microgel, has been the focus of most of my work for the past several years. pNIPAM polymer in water has a lower critical solution temperature of around 32-33 degrees Celsius - at lower temperatures, it is hydrophilic, while at higher temperatures, it becomes strongly hydrophobic. Acrylic acid, with a pK_a of about 4.4, ionizes beginning at pH higher than 3 or so, becoming fully ionized at about pH 7. PEG is hydrophilic, but its hydrophilicity has no significant temperature dependence - at very low temperatures, about 10 degrees Celsius, pNIPAM is more hydrophilic, while at higher temperatures (still below the LCST), pNIPAM becomes slightly less hydrophilic than PEG.

At low temperatures, therefore, the microgel expands to mix its pNIPAM and PEG with water as much as possible. At higher temperatures, the pNIPAM condenses to minimize its mixing with water, and in fact some research suggests that the PEG migrates to the outside of the particle to maximize its own mixing and shield the hydrophobic pNIPAM inside. Separate from the temperature, the acrylic acid begins to ionize at higher pH, drawing counterions in the solvent into the microgel and swelling it further. For low pH, the ionization is negligible and the microgels behave largely as if the acid were not present. At higher temperatures and intermediate pH between 3-6, the swelling tendency of the acid and deswelling tendency of the pNIPAM can compete, partially or completely balancing each other out. At high enough pH the ionization is strong enough to wash out the temperature-dependence completely. As shown in Fig. 1, the difference in particle radius between low pH and high temperature, and high pH, can be about a factor of 7 (which translates to more than two orders of magnitude difference in volume). R_h, the particle hydrodynamic radius, is the radius of a sphere with drag equal to that of the particles; this approximates their size since, despite being composed largely of water in their fully swollen state, they are essentially hydrodynamically opaque.

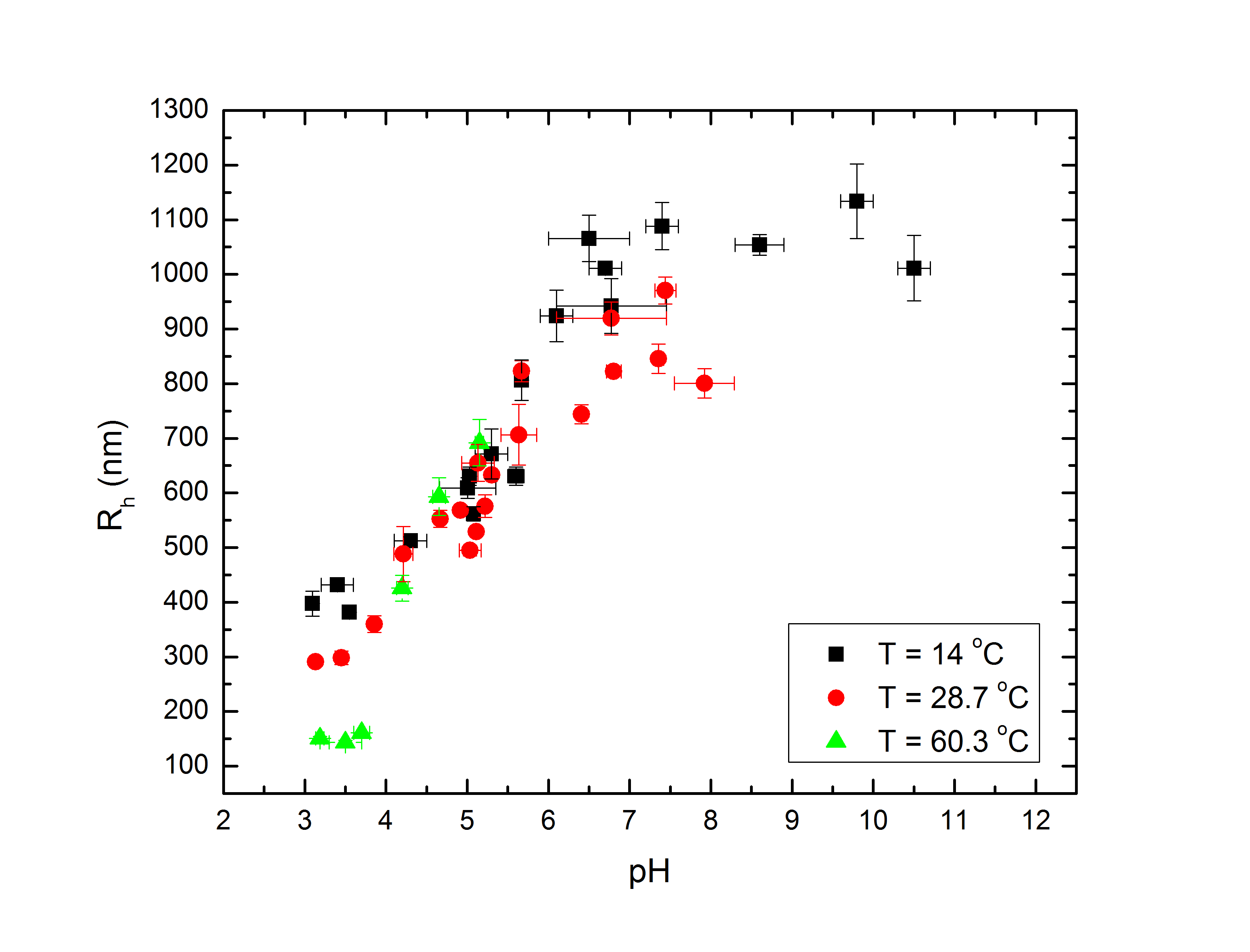
Fig 1a: Rh vs. pH at several temperatures.

Fig 1b: Rh vs. T at several pH.

I should note, however, that the specifics of these interactions are strongly dependent also on the concentration of acrylic acid, the crosslinker (PEG) density, and the details of the particle synthesis. With small enough concentrations of acrylic acid, the pH-dependence would no longer be able to completely overpower the pNIPAM at high temperatures and high pH. With more crosslinker, the particles would be less able to distend at high pH and low temperatures, and their behavior would be much less dramatic.

R_h is measured through dynamic light scattering (DLS), which in a few words measures the dyanamic correlation functions of the fluctuations in intensity of laser light scattered from the particles in the system. We use a cross-correlation spectrometer manufactured by LSI. In fact, this setup is quite sophisticated, but the theory is way too lengthy to explain here with any hope of making sense. The setup does, however, allow us to measure the correlation functions of turbid (cloudy or translucent) samples - conventional DLS is restricted to very transparent samples, but many systems our group is interested in are very turbid. DLS allows us to measure the diffusion constant of dilute samples, which is related to R_h by the Stokes-Einstein equation: $$D=\frac{k_BT}{6\pi\eta R_h}.$$ However, it also allows us to study the more complex dynamics of concentrated systems, such as sub-diffusive or ballistic particle transport, kinetic arrest in a metastable state, and aging.

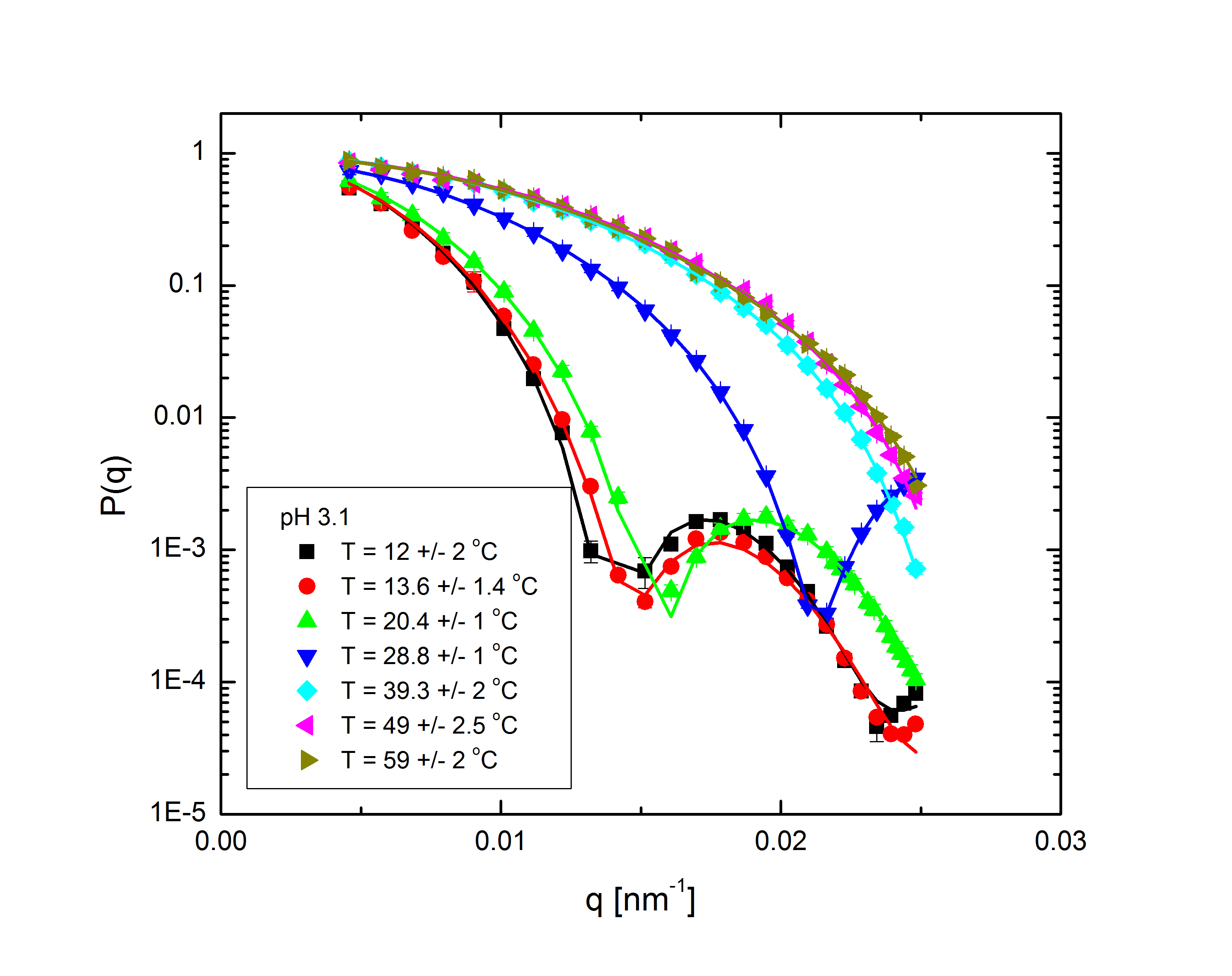
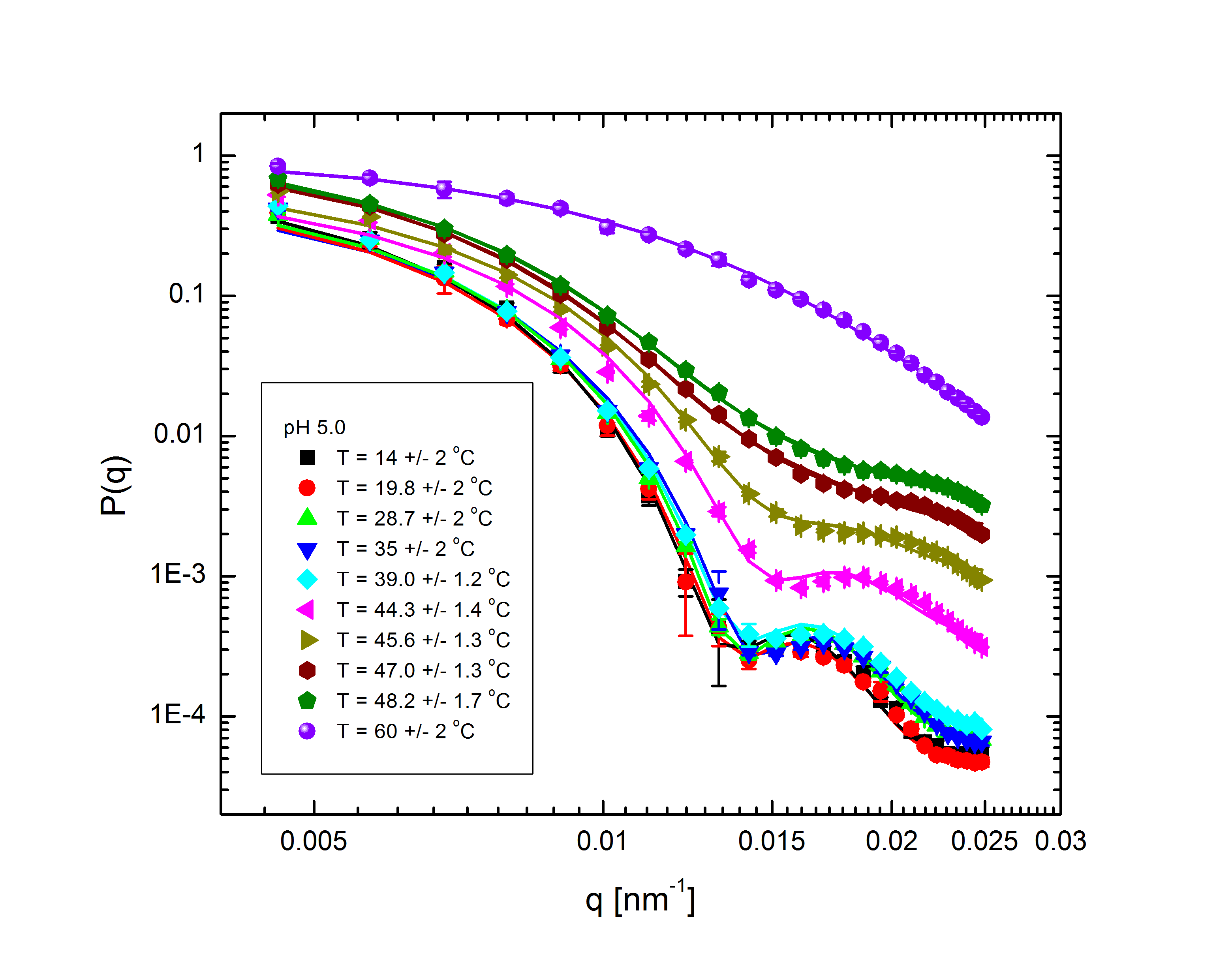
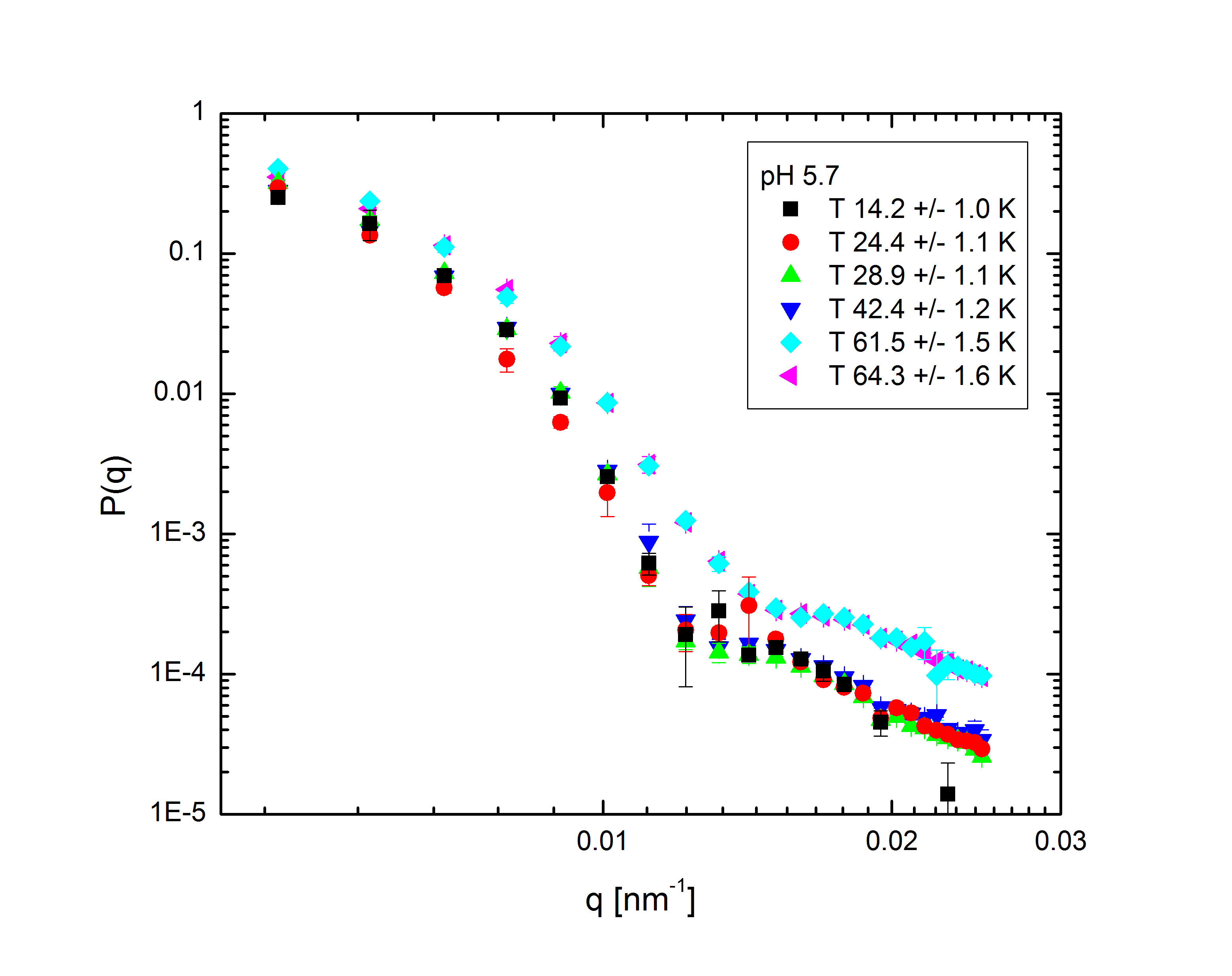
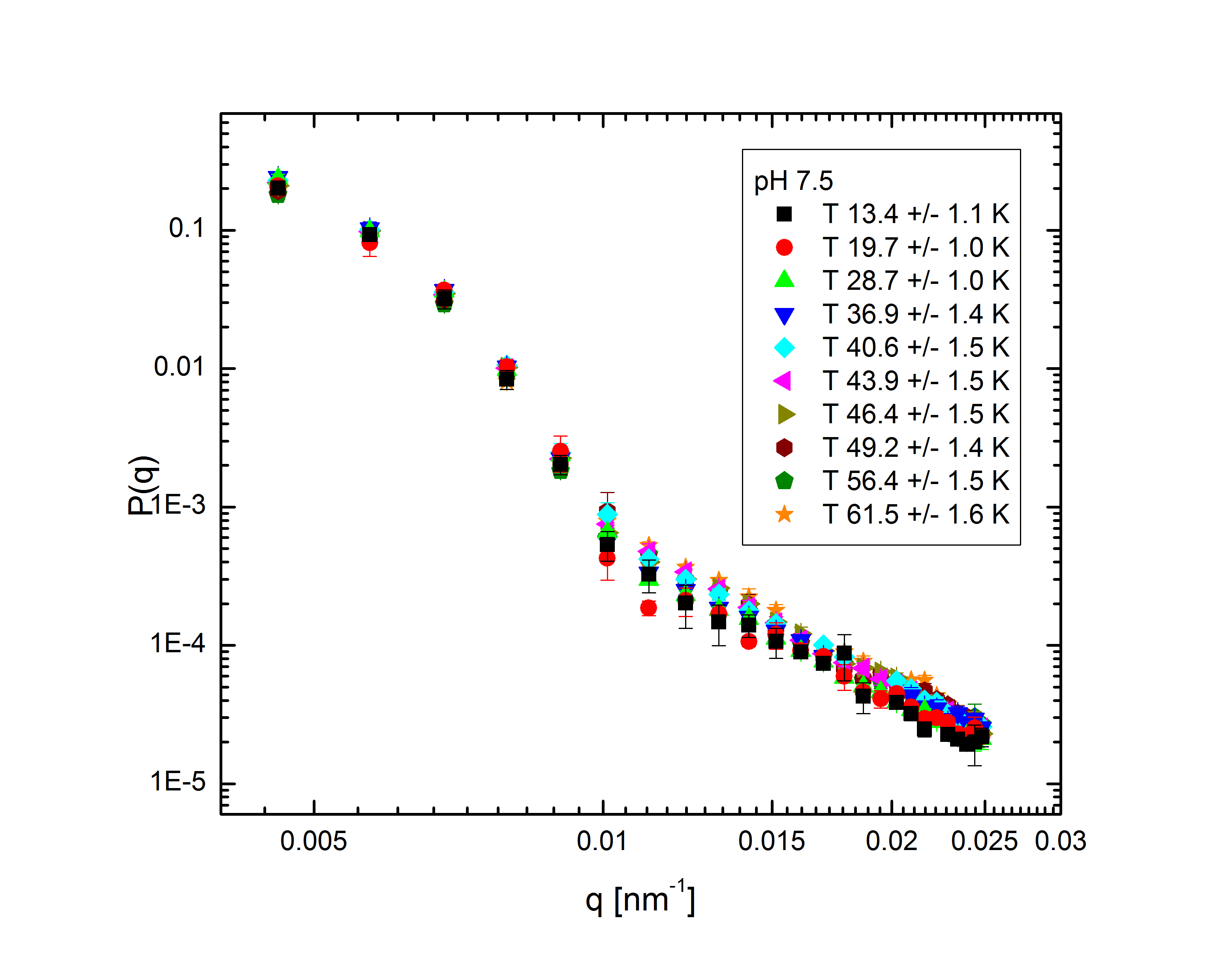
Ensemble-averaged intensity - that is, intensity averaged over all possible configurations of the system, without explicit dependence on the system's dynamics - also gives us information about the structure of the system. The profile of intensity scattered with q, the difference between the initial and final wave vectors of the scattered light, is determined entirely by the mass distribution of the particles in the system. With appropriate models to fit to the experimental data, we can back out the internal structure of the particles (size, shape, mass distribution, polydispersity) and the overall distribution of particles within the system. The intensity follows the relation $$I(q)\propto P(q)S(q),$$ where the form factor P(q) and structure factor S(q) describe the single-particle and multi-particle contributions to the intensity, respectively. Fig. 2 shows the form factors of these particles at different temperatures and pH:

Fig. 2: P(q) for pH 3.1, 5, 5.7, and 7.5 at various temperatures, normalized to P(q=0)=1.

The comparatively sharp minima in the pH 3.1 graphs indicate a somewhat well-defined particle periphery, while in the pH 7 case the form factor falls off as a power law. With the exception of the highest pH, the form factors all move towards higher q with increasing temperature; since q, a wave vector, has units of inverse length, this indicates that the particles are shrinking. In fact, the models, whose fits shown as lines in the plots, allow the particles to be very well characterized. At low pH, regardless of temperature, the particles are core-shell (a hard core surrounded by a fuzy shell of polymers) with nonzero polydispersity, described by $$P(q)\propto\int dR_{core}\exp{\left(-\frac{\left(R_{core}-\bar{R}_{core}\right)^2}{2\sigma_p^2}\right)}\left(\frac{\sin\left(qR_{core}\right)-qR_{core}\cos\left(qR_{core}\right)}{\left(qR_{core}\right)^3}\exp{\left(-\frac{\left(\sigma_{shell}q\right)^2}{2}\right)}\right)^2,$$ a function of the average core radius, the core polydispersity, and the thickness of the fuzzy shell. As the temperature increases, they transition to a star-polymer shape (extremely loosely-connected polymers spreading out from a central point), described by $$P(q)\propto \int dR_g\exp{\left(-\frac{\left(R_g-\bar{R}_g\right)^2}{2\sigma_p^2}\right)}A_1\exp{\left(-\frac{\left(qR_g\right)^2}{3}\right)}+A_2\frac{1}{q\xi}\frac{\sin\left[\mu\arctan\left(q\xi\right)\right]}{\left(1+\left(q\xi\right)^2\right)^{-\mu/2}},$$ a function of the particles' radius of gyration and polydispersity thereof, an "average blob size" within the polymer, and the polymer's fractal dimension. The models are excellent fits, with the only discrepancies occuring in the highest-q regions of the lower-pH samples. In fact, neutron scattering - which allows us to access very small length scales, and thus high q, since the deBroglie wavelength of a neutron is very small - helps us fill in the higher-q region and sheds some light on the data's departure from the model. The neutron form factor extends the above models with three terms, $$P(q)=\left(...\right)+I_0+\frac{I_{chain}}{1+\left(q\xi_1\right)^2}+\frac{I_{ex}}{\left(1+\left(q\xi_2\right)^2\right)^2}.$$ The first additional term is a constant due to the sample's incoherent scattering. The second is a Lorentzian function of the particle mesh size. The third describes correlations between inhomogeneities in the internal polymer network. Fig. 3 shows several measured form factors:

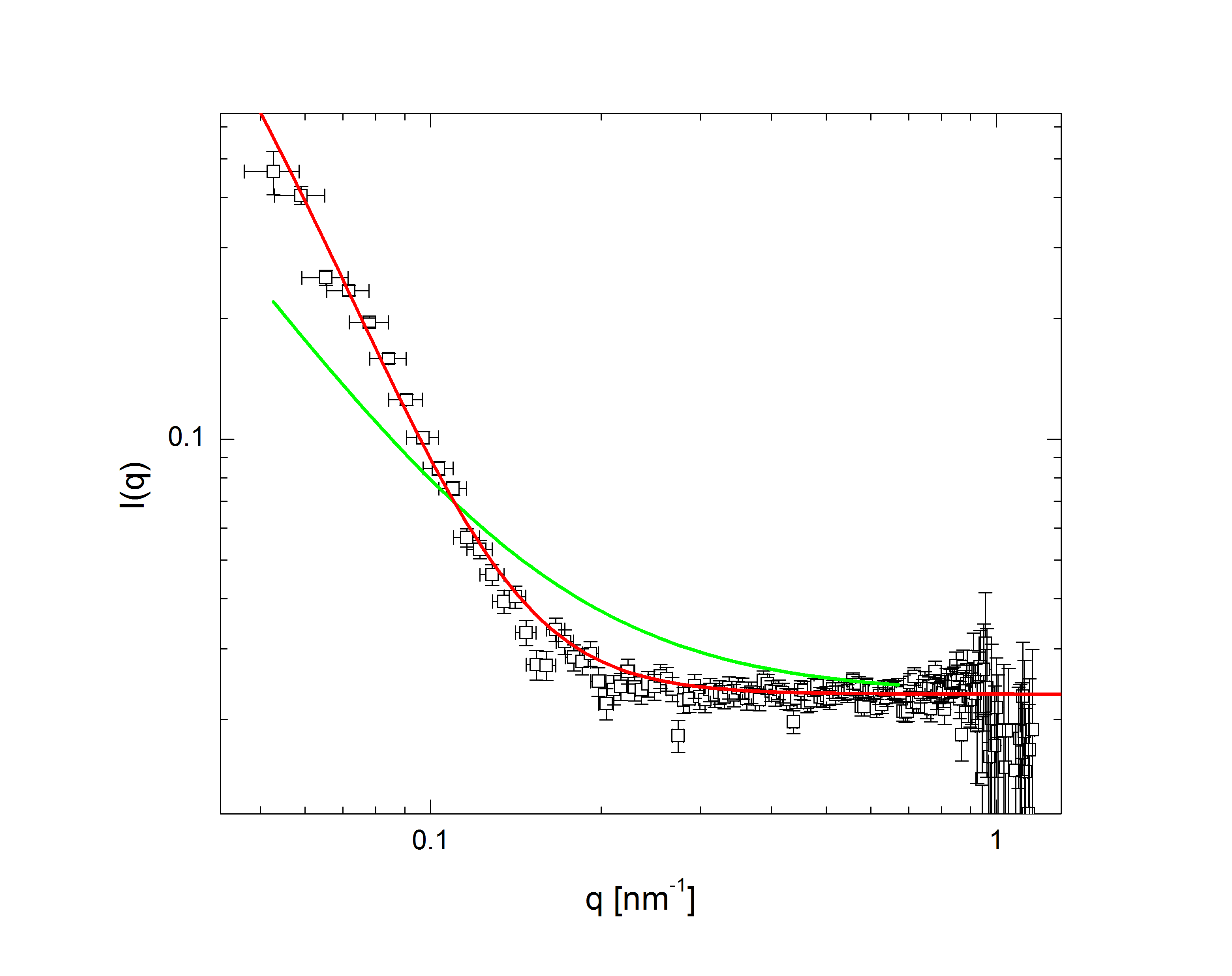
Fig 3a: pH 3, T 60 deg. C.

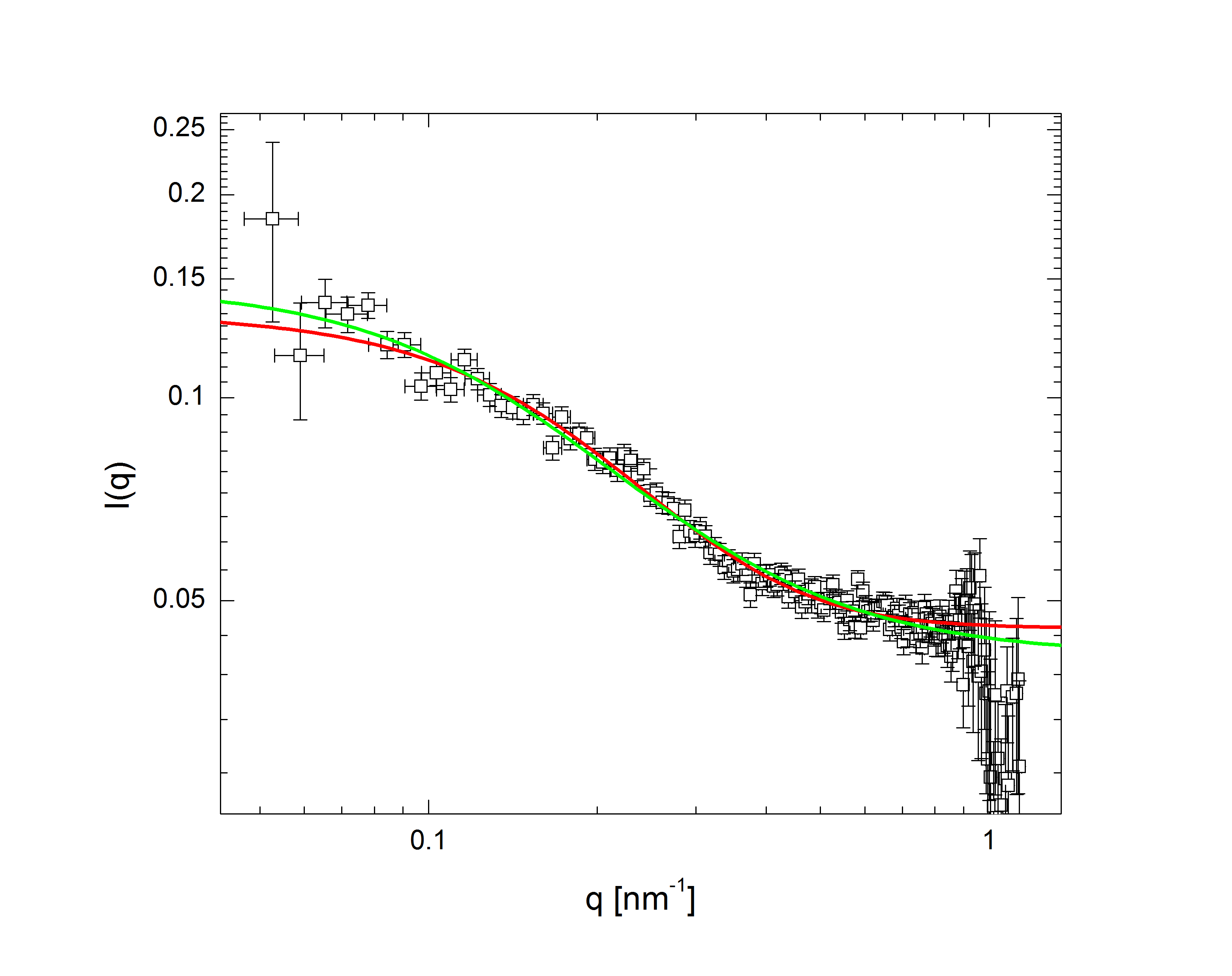
Fig 3a: pH 5, T 60 deg. C.

Fig 3a: pH 7, T 60 deg. C.

The green lines represent fits with the Lorentzian term plus a background, while in the red fits the Lorentzian has been replaced by the heterogeneity term: the internal structure of the particle is apparently more inhomogeneous over short length scales than at higher pH. Carried to lower q (the domain of q accessible in light scattering, as shown in Fig. 2), this heterogeneous density term explains the discrepancy between the data and model at higher q.