|
|
|
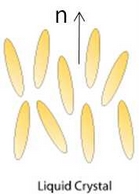
Nematic Liquid Crystals are rod-like molecules. Such molecules, if not confined, arrange themselves
parallel one to each other, allowing us to define a director field n, which represents the average
orientation of the molecules. When the Liquid Crystals are confined on a curved space, geometrical
constraints imposed by the curvature force the existence of areas where the director
field cannot be defined, areas that are called topological defects.
|
|
 Defects on spherical drops and shells have been already investigated and we are now interested in studying topology
of nematic phase on non-spherical spaces. The main reason for studying different geometries is that the number and type
of defects in a drop of Liquid Crystal is subject to the geometrical constraint that the total topological charge on the surface, i.e. the
sum of the charge of the single defects, must equal the Euler characteristic χ of the surface itself. The Euler characteristic can be expressed
in terms of the genus g of the surface Defects on spherical drops and shells have been already investigated and we are now interested in studying topology
of nematic phase on non-spherical spaces. The main reason for studying different geometries is that the number and type
of defects in a drop of Liquid Crystal is subject to the geometrical constraint that the total topological charge on the surface, i.e. the
sum of the charge of the single defects, must equal the Euler characteristic χ of the surface itself. The Euler characteristic can be expressed
in terms of the genus g of the surface 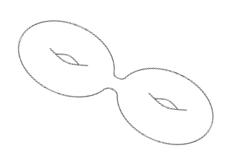 that equals the number of “handles”
of the closed surface. χ = 2(1 - g). That means that for a
sphere we will have χ = 2, on a torus χ = 0, on a figure eight χ = -2. Though on a torus the geometrical constraint allows the Liquid
Crystal to arrange in a way that doesn’t present any defect, it is possible that it will be energetically favorable for the nematic phase
to have defects: in that case we expect these defects’ charge to cancel out. The negative characteristic of the figure eight ensures that we
will need to have at least two defect of negative -2 charge. that equals the number of “handles”
of the closed surface. χ = 2(1 - g). That means that for a
sphere we will have χ = 2, on a torus χ = 0, on a figure eight χ = -2. Though on a torus the geometrical constraint allows the Liquid
Crystal to arrange in a way that doesn’t present any defect, it is possible that it will be energetically favorable for the nematic phase
to have defects: in that case we expect these defects’ charge to cancel out. The negative characteristic of the figure eight ensures that we
will need to have at least two defect of negative -2 charge.
Non-spherical drops are produced using a rotating continuous phase that exerts a viscous
force on the inner phase while it is injected into the first one using a needle. The system is stabilized using a
viscoelastic continuous phase that allows the formation of the drop while rotating, but that “freezes” the shape once the rotation is stopped.
References:
- [1] D. R. Nelson, Defects and Geometry in Condensed Matter Physics (Cambridge University Press)
- [2] V. Vitelli and D. R. Nelson, Phys. Rev. E 74, 021711 (2006)
- [3] E. Pairam A. Fernandez-Nieves, Phys. Rev. Lett. 102, 234501 (2009)
|
|



















